What is the fastest a spacecraft can get using gravity-assist?

This limitation would be imposed by the relative speed difference between the starting point and the object being used for a gravity assist.

to steal Wikipedia's example: Imagine you have a train coming at you at 50mph. You throw a ball at the front of the train at 30mph.

From your perspective, the ball was moving 30mph on the way in and 130mph on the way out (having bounced off the train). From the perspective of the train, the ball approached at 80mph and left at 80mph.

So the maximum speed, as viewed from the thrower, is a combination of the initial speed and the relative speed of the object in question.

With infinite object in perfect alignment: there is no limit other than relativity. Every exchange takes intertia from the planet and gives it to the spacecraft. The limiting factor is how much can be puller per interaction, and how many useful interactions can occur.

This is why the voyager probes were launced when they were: Jupiter, Saturn, and Uranus were aligned in such a way as to make a "grand tour" of using all three for gravity assists possible.

The one thing to keep in mind is that in order to perform a gravity-assist maneuver, you need to be able to enter a hyperbolic orbit around a given body that is moving relative to your destination. And, in order to be in such an orbit, there is a specific range of velocities for every object that you must have (dependent on mass of the object). So the fastest you can get to by gravity-assist is much less than relativistic speeds because at relativistic speeds, you would not be able to enter into a proper hyperbolic orbit.

It is true that at any high speed, a flyby constitutes a hyperbolic orbit; however, to use a gravitational slingshot, you need to enter against the object's motion and exit with the motion from that object's point of view. At relativistic speeds and for most regular bodies, your orbit would closely resemble a straight line, there could be no gain of velocity.

A good gravity assist works if you can ensure that your hyperbolic trajectory minimizes the angle $theta$ between the assisting body's trajectory and the spacecraft's exit trajectory. It is given by:

$$theta=cos^{-1}(1/e)$$

Where $e$ is the eccentricity of the orbit and must satisfy $egeq1$. From this, one can see that a parabolic trajectory is best as the exit trajectory is directly in line with the body's trajectory. We can also see that as $erightarrowinfty$, the exit trajectory is at right angles to the body's trajectory and we get no help from the assist. Additionally, as your velocity increases, it will force $e$ to become larger unless you significantly increase the mass of each subsequent object. So, for a normal assisting body, like a star or a planet, travelling past it at relativistic speeds will result in minimal orbital deviation; there will be practically no transfer of momentum, which makes for an even smaller increase in velocity.

The fastest a spacecraft can get to using gravity-assists very much depends on the largest mass of the objects you use. However, I cannot give you an estimate of a number because due to the sheer impracticality of using gravity-assists to achieve extreme velocities, we (rocket scientists) haven't ever tried computing a theoretical limit. I can guarantee you though that without using high density objects (neutron stars, black holes, etc.), no spacecraft will reach velocities near the speed of light by gravity slingshots alone.

A key limitation to how much of a velocity change can occur in a slingshot maneuver is the amount of time the spacecraft spends in the region near the planet. Change in speed is related to force x time/mass. At very high speed, the spacecraft spends only a very short time hear the planet. Moreover, at very high speeds the velocity change is very close to perpendicular to the direction of motion of the spacecraft, which means that the speed of the spacecraft won't change a lot; only its direction changes a little bit.

Another key limitation is the radius of the planet. If the planet were extremely massive and compact (like a black hole), the spacecraft could approach very close to the center of mass of the planet, and experience a large change in direction which could add up to 2x the planet's orbital speed to the spacecraft. Of course even in that case, too close an approach would result in tidal forces that could rip the spacecraft apart.

So you're right: "For example, if a spacecraft is moving at relativistic speeds, it probably won't get seriously sped up by normal-density objects."

Let's take a simple example: We have a planet and a spacecraft that is approach perpendicular to the planets motion. The spacecraft passes behind the planet, so it's path is deflected in the direction of the planets' motion. Since the spacecraft passes behind the planet, its gravity works to slow the planet down a tiny bit. So the planet looses a tiny bit of both momentum and energy. Both of these are imparted on the spacecraft, speeding it up.

Note that the only preliminary is, that the spacecraft's speed is higher than its escape speed from the planet (otherwise we would not have an encounter, but an elliptic orbit). No matter how fast the spacecraft is already, it will gain momentum and kinetic energy from the encounter.

So, there's really no cap on how fast you can get via gravity assists. It's just that the faster you go, the less time your encounter takes, reducing the amount of energy you can gain from a single encounter. But several encounters can add up their energy, as was done with the Voyagers' flyby maneuvers. Each encounter deflected the Voyagers' paths only a small bit, but the sum of the encounters sufficed to catapult the spacecrafts out of our solar system.

Now, taking this to relativistic speeds, we see that the apparent mass of the spacecraft goes up with its speed, while the encounter time has a lower limit dictated by the speed of light. Since momentum transfer is gravitational force times time, and gravitational force is proportional to mass, the relativistic spacecraft will take more momentum and energy away from the planet the faster it enters the encounter.

There are other answers there, but I wanted to give an answer in terms of the velocity of the spacecraft, the velocity of the planet, and the surface gravity of the planet.

TL;DR The largest increase in speed possible in a gravity assist is

$$ frac{2sgr}{gr + s^2} $$

where $s$ is the initial speed of the spacecraft relative to the planet, $r$ is the radius of the planet, and $g$ is the surface gravity of the planet.

A gravitational slingshot is when a spacecraft uses the gravity of a planet to gain speed relative to the solar system. In the reference frame of the planet, the spacecraft flies by it in a hyperbolic trajectory, with the same speed entering and leaving. Because the planet is moving, the speed of the craft relative to the solar system changes. This is demonstrated in the following gif from wikipedia.

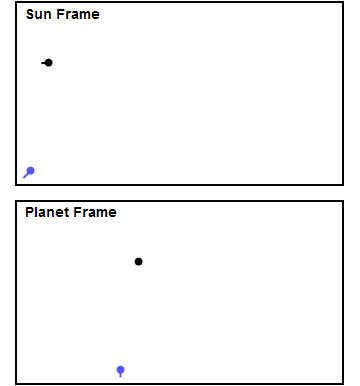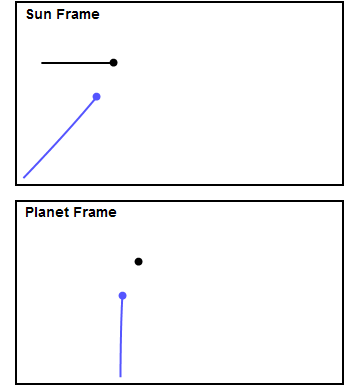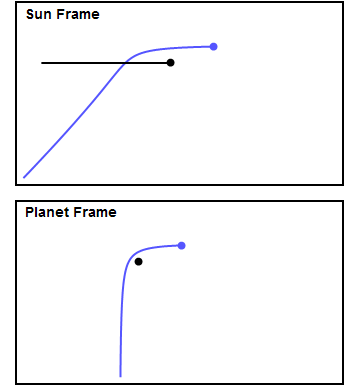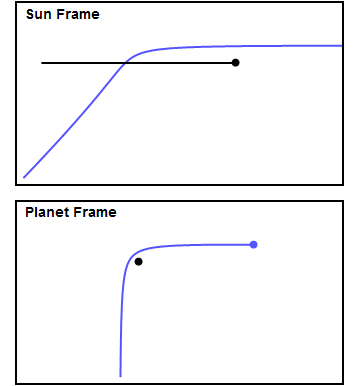
Let's analyze the motion of the spacecraft relative to the planet. We place the center of the hyperbola on the origin, and the focus of the hyperbola is the planet's center, which we place at $(c, 0)$.

Since the speed is the same long before as long after the craft leaves the planet, the maximum velocity change comes if the change in angle is maximized, which happens when the craft just skims the planets surface. Thus, if the planet's radius is $r$, the vertex of the hyperbola is at $(c - r, 0)$.

The equation of the hyperbola is of the form $$frac{x^2}{a^2} - frac{y^2}{b^2} = 1$$ with $a = c - r$, and $b^2 = c^2 - a^2$.

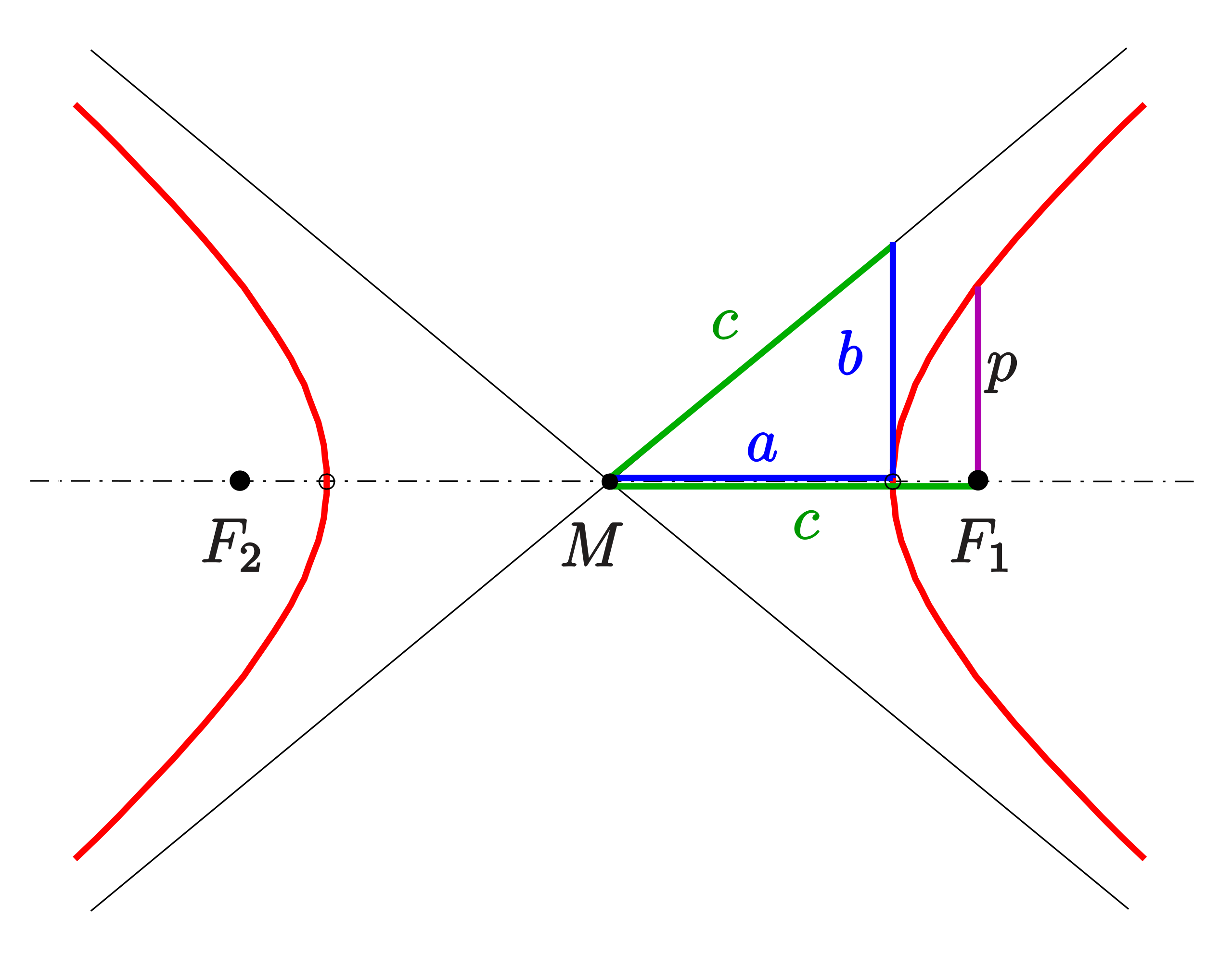
Now, the change in velocity of the craft with respect to the planet is twice the initial $x$ component of the velocity, or $2 s frac{a}{c}$. To put this in terms of the physical properties of the planet and initial speed, we will analyze the gravitational acceleration at the vertex.

Let $s$ be the speed of the craft in the limit long before the craft reaches the planet. Initially, the craft travels at speed $s$ along the asymptote $y = pm frac{b}{a} x$. This asymptote is distance $b$ from the focus. Thus, the line segment between the craft and the planet sweeps out area at the rate $frac{1}{2} b s$. By Kepler's Second law, the spacecraft sweeps out area at the same rate when it is at the vertex of the hyperbola, a distance of $c-a = r$ from the planet. So the speed $s_0$ of the craft at this time is given by $frac{1}{2} b s = frac{1}{2} r s_0$, which yields $s_0 = frac{b}{r} s$.

Differentiating the equation for the hyperbola twice with respect to time, we get

$$ (x frac{d^2x}{dt^2} + (frac{dx}{dt})^2) frac{1}{a^2} = (y frac{d^2y}{dt^2} + (frac{dy}{dt})^2) frac{1}{b^2} $$

At the vertex, we have $x = a, frac{dx}{dt} = 0, y = 0, frac{dy}{dt} = s_0$, and the gravitational acceleration is entirely in the $x$ direction, so $frac{d^2x}{dt^2} = g$, and this becomes

$$ g = s_0^2 frac{a}{b^2} $$

Or, substituting in our formula for $s_0$

$$ g = s^2 frac{a}{r^2} $$

Rearranging gives us $a$, and thus $c$ and $frac{a}{c}$, in terms of $g$, $s$, and $r$.

$$frac{a}{c} = frac{a}{a + r} = frac{1}{1 + frac{r}{a}} = frac{1}{1 + frac{s^2}{gr}} $$

So the change of velocity is

$$ frac{2sgr}{gr + s^2} $$

In the $x$-direction. If this direction is almost the same as the direction as the spacecraft's initial direction in the solar system reference frame, then this change in velocity equates to an absolute increase in speed.