What happens with the number of protons inside a wire in movement?
Physics Asked by Enrique on January 30, 2021
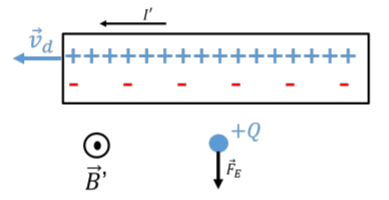
In Special Relativity we solve the problem of the moving wire with an electrical current saying the protons inside the wire have a higher density: hence the wire is not neutral anymore (and we exchange a force caused by a B field with a force caused by an E field):
But if the density of protons is higher, then the number of protons must be higher too, so changing the frame of reference is also creating new protons?
How can we explain the higher density without adding extra protons?
5 Answers
The density $rho$ of the protons increase with the factor $gamma$, but the length $L$ of the wire decreases with the same factor. So the total number of protons will be unchanged: $(gammarho)*(L/gamma) = rho L$.
Answered by md2perpe on January 30, 2021
In the frame moving with the current, the hyperplane of simultaneity (aka 'now') is tilted to the lab's future (past) in the downstream (upstream) direction.
OR: If you are in the lab frame, every time an electron leaves the wire (event B) at the downstream end, one enters to replace it at the upstream end (event A), thereby maintaining neutrality. A and B are simultaneous in the lab.
In the current frame, B occurs before A.
Answered by JEB on January 30, 2021
But if the density of protons is higher, then the number of protons must be higher too, so changing the frame of reference is also creating new protons? How can we explain the higher density without adding extra protons?
Here is an electric circuit according to an observer standing still: O Here is the same electric circuit according to an observer moving past it: 0
Let's say the observers are at the center of the O or 0. Now we can see that the moving observer sees protons packed together when he looks up or down.
To clarify what "up" means, here is a picture of an observer standing up like a stick: |
At his left and his right he sees protons being extra close to himself. That has no effect though, because the electric fields of protons have changed shape too. Still standing proton's electric field: O Moving protons electric field: 0
Answered by stuffu on January 30, 2021
In the usual presentation of this derivation, the wire is infinite in length, which means that the total number of protons in the wire is infinite. Increasing the proton density in the wire is not a problem in this case, because the "total number" of protons is "the same". No proton creation is necessary, because an infinite wire with 1 proton/unit length and an infinite wire with 2 protons/unit length both have a countably infinite number of protons.
This is very similar to the discussions about infinity that arise in "Hilbert's Hotel": in a hotel with rooms labeled 1,2,..., you can accomodate any additional number of guests you want without having to create additional rooms.
Answered by probably_someone on January 30, 2021
Normally this idea is presented in the case of a wire that is infinitely long. That gives the problem a translational symmetry and makes everything simpler. For an infinite wire, the number of protons is infinite. If you change to a different frame, the number is still infinite, but with a different density. This is similar to Hilbert's hotel: https://en.wikipedia.org/wiki/Hilbert%27s_paradox_of_the_Grand_Hotel
Answered by user275360 on January 30, 2021
Add your own answers!
Ask a Question
Get help from others!
Recent Questions
- How can I transform graph image into a tikzpicture LaTeX code?
- How Do I Get The Ifruit App Off Of Gta 5 / Grand Theft Auto 5
- Iv’e designed a space elevator using a series of lasers. do you know anybody i could submit the designs too that could manufacture the concept and put it to use
- Need help finding a book. Female OP protagonist, magic
- Why is the WWF pending games (“Your turn”) area replaced w/ a column of “Bonus & Reward”gift boxes?
Recent Answers
- Lex on Does Google Analytics track 404 page responses as valid page views?
- Jon Church on Why fry rice before boiling?
- Joshua Engel on Why fry rice before boiling?
- haakon.io on Why fry rice before boiling?
- Peter Machado on Why fry rice before boiling?