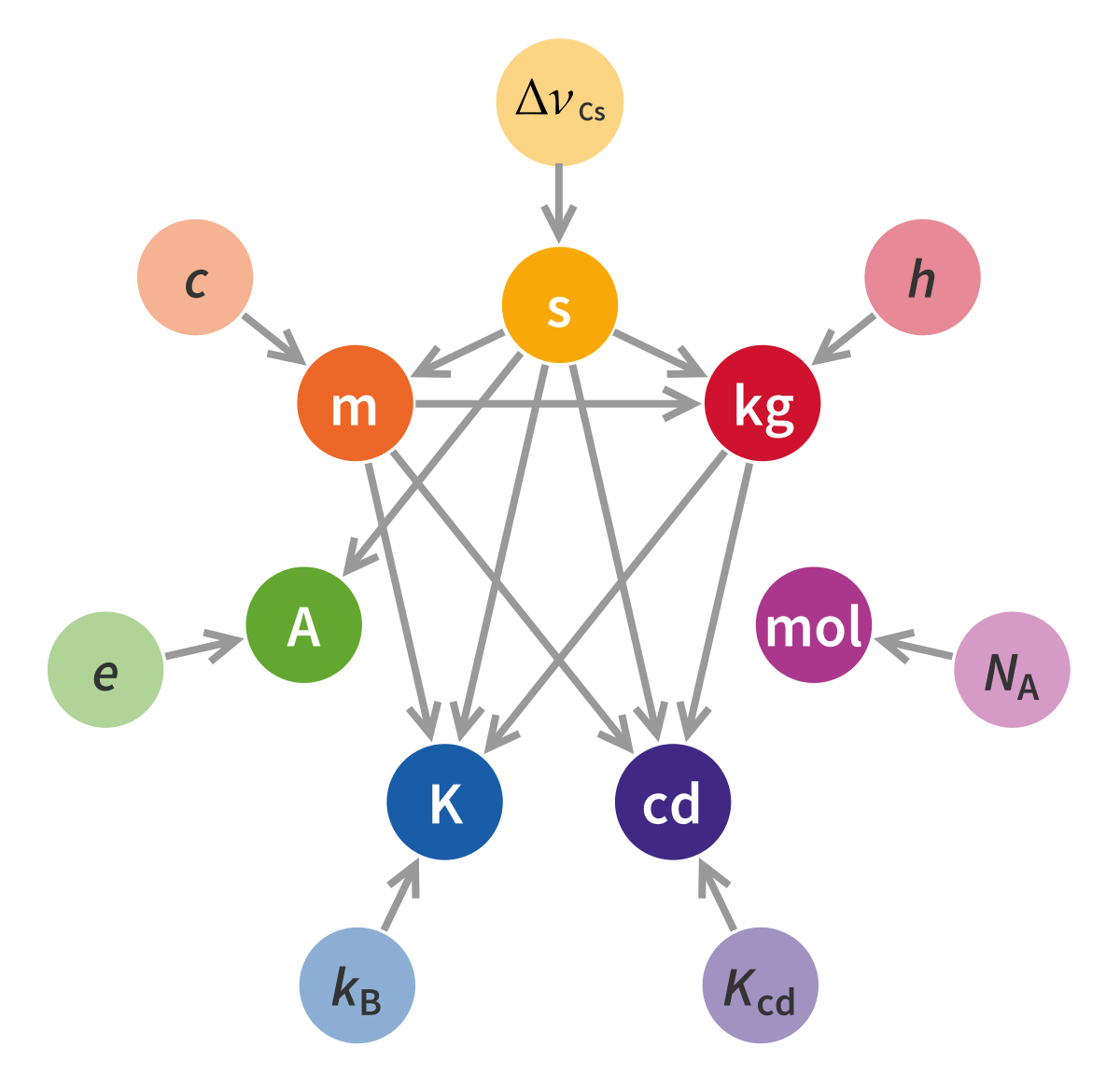
How are the seven base units related to each other?

Question

How are the seven S.I. fundamental or base units of measurement of physical quantities interrelated or dependent on other base units:

These seven SI base quantities are defined by universal constants.
For example, length is defined by speed of light, mass is defined by Plancks constant, electric is defined by electronic charge, thermodynamic temperature is defined by Boltzmann constant, amount of substance is defined by Avogadro constant, etc. which is very satisfying.
The Base quantities are those quantities on the basis of which other quantities can be expressed.
But since the base quantities are being expressed on the basis of the base quantities (as the base quantities are interdependent), the actual number of base units is possible to reduce. Some of the (or most of the ) given quantities cannot be considered fundamental or base units, if we can express them in terms of other base units. How can this be reduced?
In other words, I want to say that 'some quantities are more fundamental than other'. for example, time is more fundamental than length, and length is more fundamental than mass. ANd these are more fundamental than thermodynamic temperature and luminous intensity. What I want to do is remove these lesser fundamental quantities from the SI base unit system.
I see that mole is not connected to any other base unit. So it is certainly a 'fundamental' base unit.
I think that electric current can be eliminated, because I studied last year, that current  $I=Q/t$, where $Q$ is the electric charge in a time $t$.

Steeven · Accepted Answer

If current $I$ isn't a fundamental quantity because it can be expressed from charge $Q$ and time $t$,
$$I=frac{mathrm dQ}{mathrm dt},$$
then why is, say, time $t$ a fundamental property when it can just as well be written in terms of current and charge if we just rearrange to something along the lines of $t=Q/I$? From that logic, no quantity is ever fundamental.
The point with the chosen seven definitions of the SI unit system is that it's not important for us which quantities that are defined as fundamental. We just need a proper independent set of quantities from which all others can be described. Then it doesn't matter which we pick.
Some may "feel" more fundamental than others. Sure. That's subjective. I also personally agree that charge $Q$ "feels" more fundamental than current $I$. But it doesn't matter what I feel.
Also note that since 2019, the seven original base units in the SI unit system are no longer officially defining the unit system. Rather, seven constants of nature have been chosen, as you have shown on the diagram, which can be used to describe and define both the past base units as well as all other units. So the idea of a defining set of "core" units has been phased out. These new constants of nature might be much easier to universally accept as fundamental.

Emilio Pisanty · Answer

The relationships in the image you have quoted do not represent a "lack of fundamentality". Instead, they represent a metrological dependence in how we implement, in a real-world laboratory, the standards for the different units.
Consider, for example, the original definition of the ampere, which was in use from 1908 until 2019:

The ampere is that constant current which, if maintained in two straight parallel conductors of infinite length, of negligible circular cross-section, and placed one metre apart in vacuum, would produce between these conductors a force equal to $2×10^{-7}$ newtons per metre of length.

This is an unambiguous definition of a certain amount of current, if you have working definitions of the metre and the newton. Correspondingly, if you want to produce a high-accuracy standard of current that implements the pre-2019 definition, you require standards of length and of force to correspondingly high accuracy.
Does that mean that the ampere is any less "fundamental" than the metre and the newton? That's one possible view one could take, but it's not particularly useful. The metre and the newton are not sufficient by themselves to say anything at all about electrical measurements, and you need at least one key bit of independent information about electricity to be able to break into that territory. The definition as set out above is that key bit of information.
Could you do it differently, without invoking the metre and the newton in your definition? Not particularly, no. For one, there is an old debate regarding whether the "most fundamental" unit is the ampere of the coulomb, but that debate is moot: using 20th-century technology, the definitions of the coulomb you might come up with also hinge on the forces between charged bodies. Using modern technology, it is possible to count electrons using single-electron devices, but those are not competitive in terms of accuracy to the methods that form the core of the new SI.
In other words, there isn't really a way to postulate reasonable electrical units that do not depend on external standards. Does that mean that electricity is less "fundamental" than the dynamical triad of MKS? That's a subjective question without any objective answer $-$ it comes down to personal taste as to what you think is "fundamental".
The question that does have an objective answer is whether electrical units are independent of the dynamical MKS triad, and there we have an unambiguous, objective, positive answer: the base unit of electricity (conventionally chosen to be the ampere) is independent of the MKS triad. Specifically, it is linearly independent within the vector space of units I describe in this previous answer.
This linear independence is the key: the base units are a basis, in the linear-algebraic sense, for the vector space of units. There are many possible ways to choose a basis, and there are plenty of subjective personal reasons to argue that some other set would be more natural. The SI base units are the agreed-upon canonical basis, but that's about it.
Another reasonable question to ask here is: do we even need a canonical basis at all? and if we do need one, why stick to the previous one? As discussed in What is a base unit in the new SI, and why is the ampere one of them?, the answer is simply: because of historical continuity. The base units of the SI used to correspond very cleanly to the metrological standards used to define each units (the second to a caesium transition or to the Earth's rotation, the kilogram to the IPK, the metre to the IPM, the kelvin to the triple point of water), but that relationship has become much looser. But changing the set of base units to match the defining constants more closely would be incredibly disruptive to the existing infrastructure, to very little clear gain. So we're stuck with where we are.

How are the seven base units related to each other?

2 Answers

Add your own answers!

Ask a Question