Computing the limit $lim_{ntoinfty} cosleft( pi sqrt{4n^2 + 5n + 1} right)$ for $n in Bbb z$

Question

I want to compute the limit
$qquad lim limits_{ntoinfty} cosleft( pi sqrt{4n^2 + 5n + 1} right)$
for integer $n$. By completing the square, we can determine that this limit is equal to $ - tfrac1{sqrt2} approx -0.7071 $.
But if we don't restrict $n$ to an integer, then the limit is indeterminate / does not exist. And can be easily found by typing it on WolframAlpha. Or in Mathematica:

However, I do not know how to compute the limit (on Mathematica) with the original constraint that $n$ must be an integer.
I know that we can plot a graph on Mathematica:

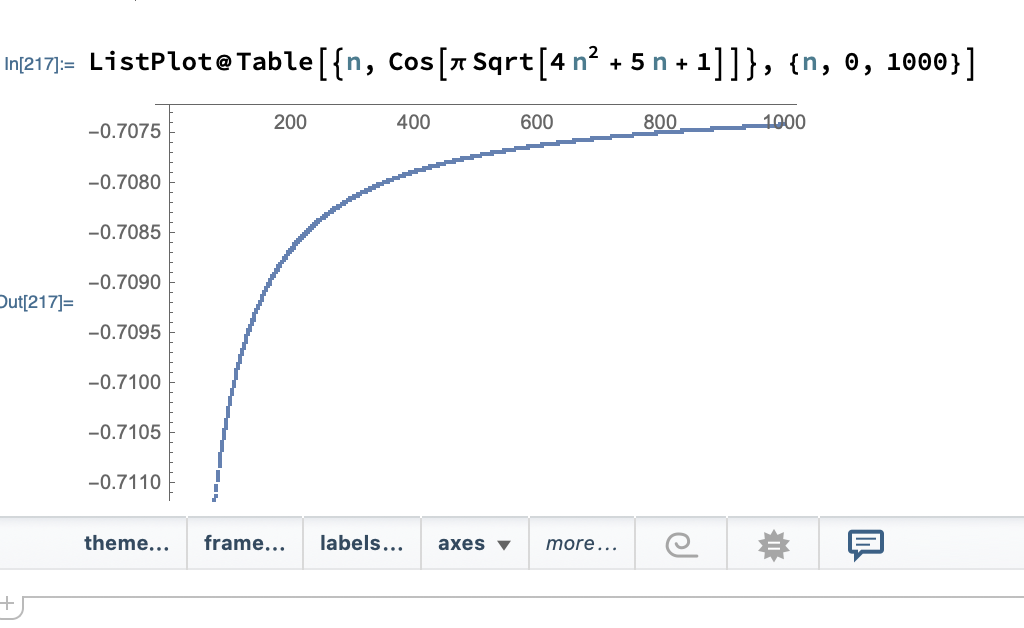
The graph suggests that the limit is equal to $-tfrac1{sqrt2} $. However, this doesn't look like a convincing result because we can't know that the limit is exactly equal to $-tfrac1{sqrt2} $.
Question: Is there a way to compute this limit in Mathematica where it spits out a single numerical value (of $-1/{sqrt2}$)?

user64494 · Accepted Answer

Improving previous answers,
DiscreteLimit[Normal[Series[Cos[Pi*Sqrt[4 n^2 + 5 n + 1]],{n,Infinity,1}]],n -> Infinity]
(*-(1/Sqrt[2])*)

Kiro · Answer

A bit of a patchwork way to show that the limit is indeed -1/Sqrt[2] for integer values of n goes as follows.
We make a series expansion of Sqrt[4n^2+5n+1] at infinity.
ser = Series[Sqrt[4 n^2 + 5 n + 1], {n, [Infinity], 3}];

Then by keeping in mind that Cos is periodic with a period of 2 Pi, we can do
Cos[Limit[ser - 2 n, n -> [Infinity]] Pi]
(*-(1/Sqrt[2])*)

where ser-2n is effectively taking the result modulo 2Pi and is valid if and only if n is an integer.
I admit that this is a bit sketchy and unsatisfactory way of doing this. While we can fully justify what we do, if we made a mistake in our thinking then the result is also wrong, so correctness of the result depends significantly on things not taken care of by Mathematica. I expect there to be more elegant ways.

Vaclav Kotesovec · Answer

We have
 Normal[Series[Sqrt[4*n^2 + 5 n + 1], {n, Infinity, 1}]]
 (* 5/4 - 9/(64 n) + 2 n *)

If n tends to infinity, the expression above tends to
 Cos[(5/4 + 2 n) [Pi]]

For integer n is the limit equal to
$cos left(frac{5 pi }{4}right)=-frac{1}{sqrt{2}}$

A little mouse on the pampas · Answer

DiscreteAsymptotic[Cos[π*
   Sqrt[4*n^2 + 5 n + 1]], n -> Infinity](*-(1/Sqrt[2])*)

Computing the limit $lim_{ntoinfty} cosleft( pi sqrt{4n^2 + 5n + 1} right)$ for $n in Bbb z$

4 Answers

Add your own answers!

Ask a Question